Volumetric Demand and Conjunctive Screening with echoice2
Source:vignettes/Modeling_volumetric_demand.Rmd
Modeling_volumetric_demand.RmdBackground
The case study described in this vignette deals with demand for consumer packaged goods where consumers commonly purchase multiple goods at the same time and employ screening rules to reduce the complexity of their choices. The original data came from a volumetric conjoint experiment about frozen pizzas, where buyers frequently buy more than one unit per purchase occasion. The example data included in this package has been designed to yield similar results.
Installation
The echoice2 package is available from CRAN and GitHub.
To install from CRAN, run:
install.packages("echoice2")To install the latest development version from GitHub run:
remotes::install_github("ninohardt/echoice2")Getting started
Load the package.
Key functions for using the package are:
-
vd_est_vdm: Estimating the “standard” volumetric demand model -
vd_est_vdm_screen: Estimating volumetric demand model with screening -
vd_dem_vdm: Demend predictions for the “standard” volumetric demand model -
vd_dem_vdm_screen: Demend predictions for the volumetric demand model with screening
Functions that relate to discrete demand start in dd_,
while functions for volumetric demand start in vd_.
Estimation functions continue in est, demand simulators in
dem. Universal functions (discrete and volumetric choice)
start in ec_.
Data
Choice data should be provided in a `long’ format tibble or data.frame, i.e. one row per alternative, choice task and respondent.
It should contain the following columns
-
id(integer; respondent identifier) -
task(integer; task number) -
alt(integer; alternative #no within task) -
x(double; quantity purchased) -
p(double; price) - attributes defining the choice alternatives (factor, ordered) and/or
- continuous attributes defining the choice alternatives (numeric)
By default, it is assumed that respondents were able to choose the ‘outside good’, i.e. there is a ‘no-choice’ option. The no-choice option should not be explicitly stated, i.e. there is no “no-choice-level” in any of the attributes. This differs common practice in discrete choice modeling, however, the implicit outside good is consistent with both volumetric and discrete choice models based on economic assumptions.
Dummy-coding is performed automatically to ensure consistency between
estimation and prediction, and to set up screening models in a
consistent manner. Categorical attributes should therefore be provided
as factor or ordered, and not be
dummy-coded.
Let’s consider an example dataset from a volumetric conjoint about frozen pizza:
data(pizza)
head(pizza)
#> # A tibble: 6 × 11
#> id task alt x p brand size crust topping coverage cheese
#> <int> <int> <int> <dbl> <dbl> <fct> <fct> <fct> <fct> <fct> <fct>
#> 1 2 1 1 0 4.5 Tony forOne StufCr Pepperoni densetop realcheese
#> 2 2 1 2 0 4.5 DiGi ForTwo Thin Surp densetop NoInfo
#> 3 2 1 3 0 3 Fresc ForTwo TrCr Veg ModCover NoInfo
#> 4 2 1 4 0 1.75 Priv forOne RisCr HI ModCover realcheese
#> 5 2 1 5 2 3.25 Tomb forOne TrCr Cheese ModCover NoInfo
#> 6 2 1 6 0 3.75 RedBa ForTwo StufCr PepSauHam densetop realcheeseThere are n_distinct(pizza$id) unique despondents who
respond to pizza$task %>% n_distinct() choice tasks with
n_distinct(pizza$alt) alternatives each. The convenience
functionec_summarize_attrlvls provides a quick glance at
the attributes and levels (for categorical attributes). The function
uses standard ‘tidyverse’ functions to generate that summary.
pizza %>% ec_summarize_attrlvls
#> # A tibble: 6 × 2
#> attribute levels
#> <chr> <chr>
#> 1 brand DiGi, Fresc, Priv, RedBa, Tomb, Tony
#> 2 size forOne, ForTwo
#> 3 crust Thin, RisCr, StufCr, TrCr
#> 4 topping Pepperoni, Cheese, HI, PepSauHam, Surp, Veg
#> 5 coverage densetop, ModCover
#> 6 cheese NoInfo, realcheeseLooking across choice tasks, we can see that sometimes respondents choose 0 quantity of all alternatives in a choice task. In this case, their entire budget is allocated towards the ‘outside good’, which is not explicitly stated in the data. Even when they choose any positive quantity of alternatives, they would still consume some amount of outside good. Volumetric demand models regularly assume that respondents never consume their entire category budget, there will always some amount left (and if it is only a fraction of a cent).
pizza %>%
group_by(id, task) %>%
summarise(x_total = sum(x), .groups = "keep") %>%
group_by(x_total) %>% count(x_total)
#> # A tibble: 22 × 2
#> # Groups: x_total [22]
#> x_total n
#> <dbl> <int>
#> 1 0 282
#> 2 1 316
#> 3 2 330
#> 4 3 207
#> 5 4 233
#> 6 5 102
#> 7 6 406
#> 8 7 36
#> 9 8 52
#> 10 9 15
#> # … with 12 more rowsThe long “tidy” data structure makes it easy to work with choice data. Using just a few lines of code, we can visualize the distribution of quantity demanded per choice task, on average. From this, we can clearly see that respondents frequently buy more than one unit of frozen pizza, which suggest that indeed a volumetric choice experiment is more realistic than a discrete choice one.
pizza %>%
group_by(id, task) %>%
summarise(sum_x=sum(x), .groups = "keep") %>%
group_by(id) %>%
summarise(mean_x=mean(sum_x), .groups = "keep") %>%
ggplot(aes(x=mean_x)) +
geom_density(fill="lightgrey", linewidth=1) +
geom_vline(xintercept=1, linewidth=2, color="darkred") +
theme_minimal() +
xlab("Average units per task")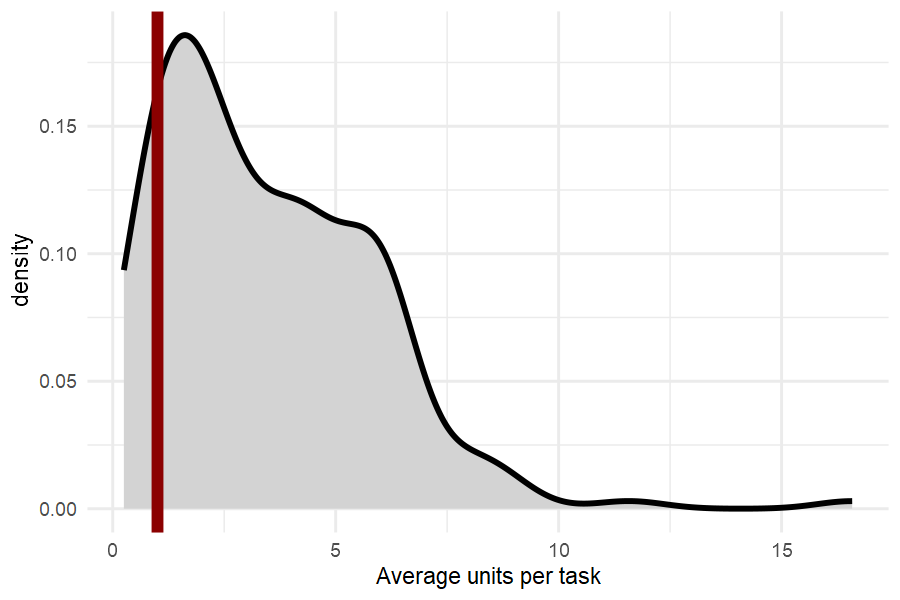
Holdout
For hold-out validation, we keep 1 task per respondent. In v-fold cross-validation, this is done several times. However, each re-run of the model may take a while. For this example, we only use 1 set of holdout tasks. Hold-out evaluations results may vary slightly between publications that discuss this dataset.
#randomly assign hold-out group, use seed for reproducible plot
set.seed(1.2335252)
pizza_ho_tasks=
pizza %>%
distinct(id,task) %>%
mutate(id=as.integer(id))%>%
group_by(id) %>%
summarise(task=sample(task,1), .groups = "keep")
set.seed(NULL)
#calibration data
pizza_cal= pizza %>% mutate(id=as.integer(id)) %>%
anti_join(pizza_ho_tasks, by=c('id','task'))
#'hold-out' data
pizza_ho= pizza %>% mutate(id=as.integer(id)) %>%
semi_join(pizza_ho_tasks, by=c('id','task'))Estimation
Estimate both models using at least 200,000 draws. Saving
each 50th or 100th draw is sufficient. The vd_est_vdm fits
the compensatory volumetric demand model, while
vd_est_vdm_screen fits the model with attribute-based
conjunctive screening. Using the error_dist argument, the
type of error distribution can be specified. While KHKA 2022
assume Normal-distributed errors, here we assume Extreme Value Type 1
errors.
#compensatory
out_pizza_cal = pizza_cal %>% vd_est_vdm(R=200000, keep=50, error_dist = "EV1")
dir.create("draws")
save(out_pizza_cal,file='draws/out_pizza_cal.rdata')
#conjunctive screening
out_pizza_screening_cal = pizza_cal %>% vd_est_vdm_screen(R=200000, keep=50, error_dist = "EV1")
save(out_pizza_screening_cal,file='draws/out_pizza_screening_cal.rdata')Diagnostics
Quick check of convergence, or stationarity of the traceplots.
Compensatory:
out_pizza_cal %>% ec_trace_MU(burnin = 100)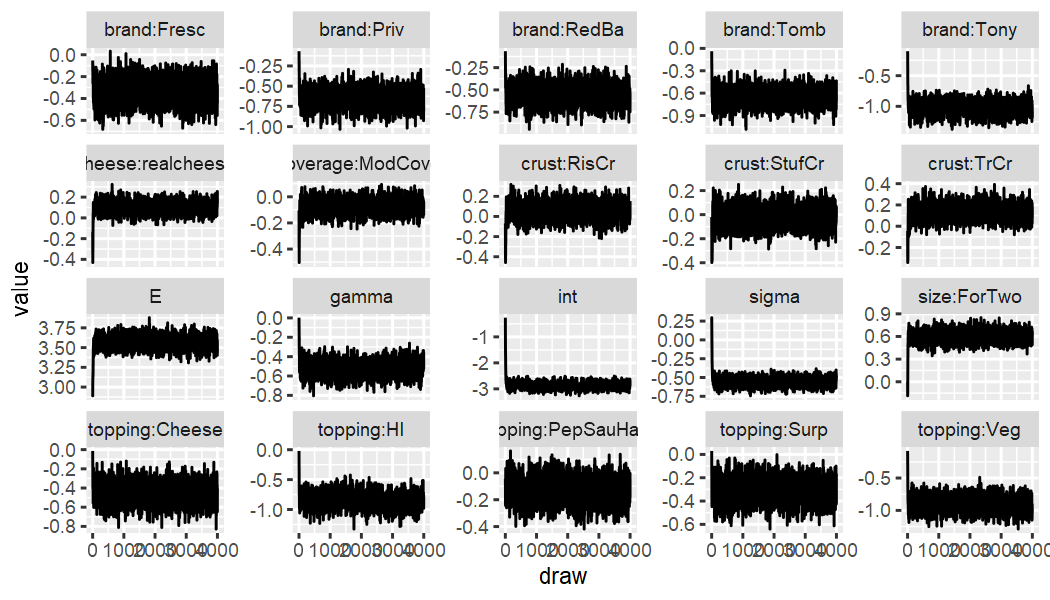
Conjunctive Screening:
out_pizza_screening_cal %>% ec_trace_MU(burnin = 100)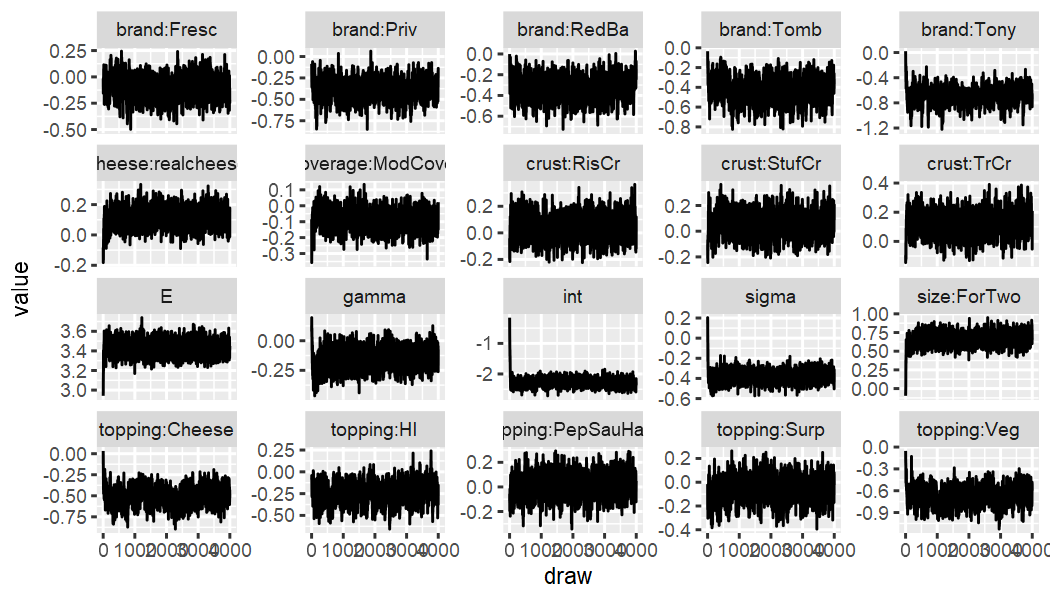
Distribution of Log-likehoods to check for outlier respondents:
vd_LL_vdm(out_pizza_cal ,pizza_cal, fromdraw = 3000) %>%
apply(1,mean) %>% tibble(LL=.) %>%
ggplot(aes(x=LL)) +
geom_density(fill="lightgrey", linewidth=1) + theme_minimal() +
xlab("Individual average Log-Likelihood")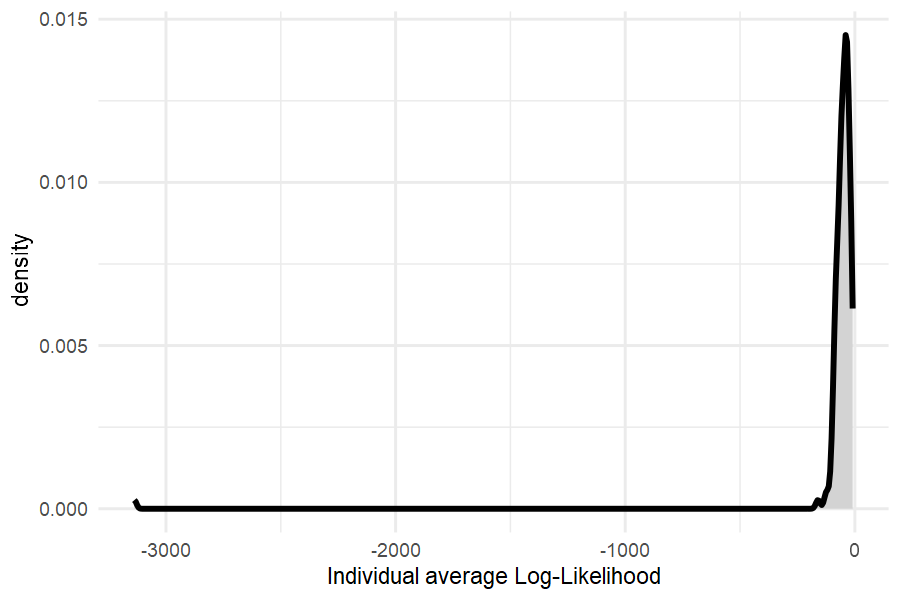
Here the left tail looks fine, and there do not appear to be extremely “bad” responders.
Fit
Holdout
Now, we compare “holdout”-fit. First, posterior means of predictions
are obtained via vd_dem_summarise, then the Mean Squared
Error (MSE) and Mean Absolute Error (MAE) are computed and average
across respondents. For illustration purposes, only one fold is used for
holdout fit. Moreover, only 5000 draws and 5000 simulated error terms
are used.
#generate predictions
ho_dem_vd=
pizza_ho %>%
prep_newprediction(pizza_cal) %>%
vd_dem_vdm(out_pizza_cal,
ec_gen_err_ev1(pizza_ho, out_pizza_cal, seed=101.1))
ho_dem_vdscreen=
pizza_ho %>%
prep_newprediction(pizza_cal) %>%
vd_dem_vdm_screen(out_pizza_screening_cal,
epsilon_not=ec_gen_err_ev1(pizza_ho, out_pizza_screening_cal, seed=101.1))
#evaluate
list(compensatory = ho_dem_vd,
conjunctive = ho_dem_vdscreen) %>%
purrr::map_dfr(.%>%
vd_dem_summarise() %>% dplyr::select(id:cheese, .pred=`E(demand)`) %>%
mutate(pmMSE=(x-.pred)^2,
pmMAE=abs(x-.pred)) %>%
summarise(MSE=mean(pmMSE),
MAE=mean(pmMAE)),
.id = 'model') -> holdout_fits
holdout_fits
#> # A tibble: 2 × 3
#> model MSE MAE
#> <chr> <dbl> <dbl>
#> 1 compensatory 0.669 0.418
#> 2 conjunctive 0.598 0.387Estimates
Part-Worths
Using ec_estimates_MU it is easy to obtain the “upper
level” posterior means of the key parameters.
out_pizza_cal %>% ec_estimates_MU()
#> # A tibble: 20 × 12
#> attribute lvl par mean sd `CI-5%` `CI-95%` sig model error reference_lvl parameter
#> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <lgl> <chr> <chr> <chr> <chr>
#> 1 <NA> <NA> int -2.87 0.143 -3.06 -2.67 TRUE VD-comp EV1 <NA> int
#> 2 brand Fresc brand:Fresc -0.331 0.100 -0.500 -0.166 TRUE VD-comp EV1 DiGi Fresc
#> 3 brand Priv brand:Priv -0.652 0.106 -0.823 -0.479 TRUE VD-comp EV1 DiGi Priv
#> 4 brand RedBa brand:RedBa -0.547 0.101 -0.715 -0.383 TRUE VD-comp EV1 DiGi RedBa
#> 5 brand Tomb brand:Tomb -0.651 0.104 -0.824 -0.482 TRUE VD-comp EV1 DiGi Tomb
#> 6 brand Tony brand:Tony -1.02 0.108 -1.20 -0.853 TRUE VD-comp EV1 DiGi Tony
#> 7 size ForTwo size:ForTwo 0.602 0.0757 0.489 0.720 TRUE VD-comp EV1 forOne ForTwo
#> 8 crust RisCr crust:RisCr 0.0555 0.0810 -0.0759 0.184 FALSE VD-comp EV1 Thin RisCr
#> 9 crust StufCr crust:StufCr -0.0171 0.0790 -0.148 0.109 FALSE VD-comp EV1 Thin StufCr
#> 10 crust TrCr crust:TrCr 0.134 0.0706 0.0241 0.246 TRUE VD-comp EV1 Thin TrCr
#> 11 topping Cheese topping:Cheese -0.453 0.101 -0.621 -0.289 TRUE VD-comp EV1 Pepperoni Cheese
#> 12 topping HI topping:HI -0.851 0.121 -1.05 -0.656 TRUE VD-comp EV1 Pepperoni HI
#> 13 topping PepSauHam topping:PepSauHam -0.128 0.0850 -0.271 0.0123 FALSE VD-comp EV1 Pepperoni PepSauHam
#> 14 topping Surp topping:Surp -0.314 0.0931 -0.470 -0.159 TRUE VD-comp EV1 Pepperoni Surp
#> 15 topping Veg topping:Veg -0.900 0.109 -1.08 -0.731 TRUE VD-comp EV1 Pepperoni Veg
#> 16 coverage ModCover coverage:ModCover -0.0727 0.0536 -0.156 0.0118 FALSE VD-comp EV1 densetop ModCover
#> 17 cheese realcheese cheese:realcheese 0.100 0.0552 0.0167 0.186 TRUE VD-comp EV1 NoInfo realcheese
#> 18 <NA> <NA> sigma -0.557 0.0637 -0.645 -0.468 TRUE VD-comp EV1 <NA> sigma
#> 19 <NA> <NA> gamma -0.525 0.0762 -0.646 -0.404 TRUE VD-comp EV1 <NA> gamma
#> 20 <NA> <NA> E 3.57 0.0788 3.44 3.69 TRUE VD-comp EV1 <NA> E
out_pizza_screening_cal %>% ec_estimates_MU()
#> # A tibble: 20 × 12
#> attribute lvl par mean sd `CI-5%` `CI-95%` sig model error reference_lvl parameter
#> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <lgl> <chr> <chr> <chr> <chr>
#> 1 <NA> <NA> int -2.27 0.146 -2.47 -2.07 TRUE VD-conj-pr EV1 <NA> int
#> 2 brand Fresc brand:Fresc -0.0989 0.103 -0.266 0.0700 FALSE VD-conj-pr EV1 DiGi Fresc
#> 3 brand Priv brand:Priv -0.381 0.116 -0.577 -0.197 TRUE VD-conj-pr EV1 DiGi Priv
#> 4 brand RedBa brand:RedBa -0.325 0.105 -0.501 -0.155 TRUE VD-conj-pr EV1 DiGi RedBa
#> 5 brand Tomb brand:Tomb -0.426 0.113 -0.619 -0.250 TRUE VD-conj-pr EV1 DiGi Tomb
#> 6 brand Tony brand:Tony -0.684 0.132 -0.904 -0.477 TRUE VD-conj-pr EV1 DiGi Tony
#> 7 size ForTwo size:ForTwo 0.658 0.0834 0.533 0.785 TRUE VD-conj-pr EV1 forOne ForTwo
#> 8 crust RisCr crust:RisCr 0.0475 0.0814 -0.0840 0.181 FALSE VD-conj-pr EV1 Thin RisCr
#> 9 crust StufCr crust:StufCr 0.0600 0.0850 -0.0839 0.196 FALSE VD-conj-pr EV1 Thin StufCr
#> 10 crust TrCr crust:TrCr 0.126 0.0745 0.00479 0.249 TRUE VD-conj-pr EV1 Thin TrCr
#> 11 topping Cheese topping:Cheese -0.508 0.103 -0.679 -0.341 TRUE VD-conj-pr EV1 Pepperoni Cheese
#> 12 topping HI topping:HI -0.244 0.115 -0.434 -0.0599 TRUE VD-conj-pr EV1 Pepperoni HI
#> 13 topping PepSauHam topping:PepSauHam 0.0116 0.0910 -0.136 0.166 FALSE VD-conj-pr EV1 Pepperoni PepSauHam
#> 14 topping Surp topping:Surp -0.0571 0.0964 -0.218 0.0996 FALSE VD-conj-pr EV1 Pepperoni Surp
#> 15 topping Veg topping:Veg -0.668 0.120 -0.866 -0.479 TRUE VD-conj-pr EV1 Pepperoni Veg
#> 16 coverage ModCover coverage:ModCover -0.0872 0.0575 -0.182 0.00412 FALSE VD-conj-pr EV1 densetop ModCover
#> 17 cheese realcheese cheese:realcheese 0.115 0.0596 0.0193 0.212 TRUE VD-conj-pr EV1 NoInfo realcheese
#> 18 <NA> <NA> sigma -0.378 0.0588 -0.468 -0.290 TRUE VD-conj-pr EV1 <NA> sigma
#> 19 <NA> <NA> gamma -0.153 0.0821 -0.292 -0.0204 TRUE VD-conj-pr EV1 <NA> gamma
#> 20 <NA> <NA> E 3.43 0.0716 3.31 3.55 TRUE VD-conj-pr EV1 <NA> EScreening probabilities
Using ec_estimates_screen, screening probabilities be
obtained.
out_pizza_screening_cal %>% ec_estimates_screen()
#> # A tibble: 22 × 8
#> attribute lvl par mean sd `CI-5%` `CI-95%` limit
#> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 brand DiGi brand:DiGi 0.0205 0.0377 0.00166 0.0452 NA
#> 2 brand Fresc brand:Fresc 0.118 0.0423 0.0641 0.172 NA
#> 3 brand Priv brand:Priv 0.167 0.0478 0.0981 0.236 NA
#> 4 brand RedBa brand:RedBa 0.130 0.0437 0.0752 0.189 NA
#> 5 brand Tomb brand:Tomb 0.171 0.0494 0.100 0.239 NA
#> 6 brand Tony brand:Tony 0.269 0.0556 0.180 0.353 NA
#> 7 cheese NoInfo cheese:NoInfo 0.00854 0.0353 0.000366 0.0175 NA
#> 8 cheese realcheese cheese:realcheese 0.00881 0.0354 0.000402 0.0187 NA
#> 9 coverage ModCover coverage:ModCover 0.00879 0.0353 0.000427 0.0180 NA
#> 10 coverage densetop coverage:densetop 0.0102 0.0356 0.000506 0.0229 NA
#> # … with 12 more rowsFor a boxplot of screening parameters, use
ec_boxplot_screen.
out_pizza_screening_cal %>% ec_boxplot_screen()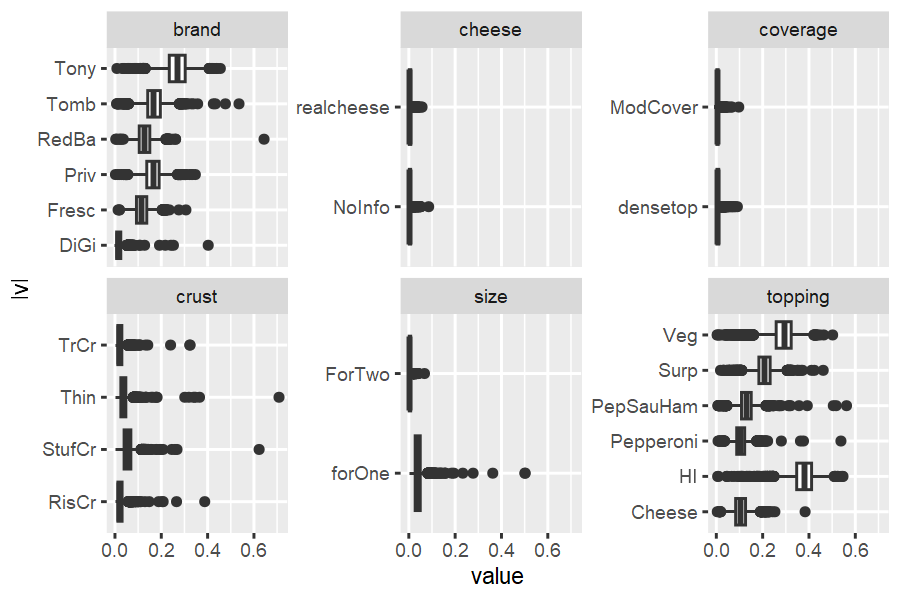
Comparisons
Side-by-side part-worths of the volumetric demand models can be
obtained by using ec_estimates_MU inside
purrr::map.
list(compensatory=out_pizza_cal,
conjunctive =out_pizza_screening_cal) %>%
purrr::map_dfr(ec_estimates_MU, .id='model') %>%
dplyr::select(model, attribute, lvl, par, mean) %>%
tidyr::pivot_wider(names_from = model, values_from = mean)
#> # A tibble: 20 × 5
#> attribute lvl par compensatory conjunctive
#> <chr> <chr> <chr> <dbl> <dbl>
#> 1 <NA> <NA> int -2.87 -2.27
#> 2 brand Fresc brand:Fresc -0.331 -0.0989
#> 3 brand Priv brand:Priv -0.652 -0.381
#> 4 brand RedBa brand:RedBa -0.547 -0.325
#> 5 brand Tomb brand:Tomb -0.651 -0.426
#> 6 brand Tony brand:Tony -1.02 -0.684
#> 7 size ForTwo size:ForTwo 0.602 0.658
#> 8 crust RisCr crust:RisCr 0.0555 0.0475
#> 9 crust StufCr crust:StufCr -0.0171 0.0600
#> 10 crust TrCr crust:TrCr 0.134 0.126
#> 11 topping Cheese topping:Cheese -0.453 -0.508
#> 12 topping HI topping:HI -0.851 -0.244
#> 13 topping PepSauHam topping:PepSauHam -0.128 0.0116
#> 14 topping Surp topping:Surp -0.314 -0.0571
#> 15 topping Veg topping:Veg -0.900 -0.668
#> 16 coverage ModCover coverage:ModCover -0.0727 -0.0872
#> 17 cheese realcheese cheese:realcheese 0.100 0.115
#> 18 <NA> <NA> sigma -0.557 -0.378
#> 19 <NA> <NA> gamma -0.525 -0.153
#> 20 <NA> <NA> E 3.57 3.43We can see that Hawaii topping and Tony brand receive higher average utilities in the screening model, because non-purchases of these Pizzas is explained by screening, not by the preference model.
list(compensatory=out_pizza_cal,
conjunctive =out_pizza_screening_cal) %>%
purrr::map_dfr(ec_estimates_MU,.id='model') %>%
dplyr::select(model, attribute, lvl, par, mean) %>%
tidyr::pivot_wider(names_from = model, values_from = mean) %>%
transmute(par, difference=conjunctive-compensatory) %>% arrange(desc(difference))
#> # A tibble: 20 × 2
#> par difference
#> <chr> <dbl>
#> 1 topping:HI 0.606
#> 2 int 0.595
#> 3 gamma 0.372
#> 4 brand:Tony 0.334
#> 5 brand:Priv 0.272
#> 6 topping:Surp 0.257
#> 7 topping:Veg 0.232
#> 8 brand:Fresc 0.232
#> 9 brand:Tomb 0.225
#> 10 brand:RedBa 0.222
#> 11 sigma 0.179
#> 12 topping:PepSauHam 0.140
#> 13 crust:StufCr 0.0771
#> 14 size:ForTwo 0.0557
#> 15 cheese:realcheese 0.0151
#> 16 crust:TrCr -0.00771
#> 17 crust:RisCr -0.00800
#> 18 coverage:ModCover -0.0145
#> 19 topping:Cheese -0.0545
#> 20 E -0.134Demand Curves
Elasticities in volumetric demand models are not constant. To better understand implications of pricing decisions, demand curves can be a helpful tool.
The ec_demcurve function can be applied to all demand
simulators. Based of an initial market scenario, it generates a series
of scenarios where the price of a focal product is changed over an
interval. It then runs the demand simulator several times, and we can
use the output to draw a demand curve.
Pre-simulating error terms using ec_gen_err_ev1 helps to
smooth these demand curves. It generates one error term per draw for
each of the alternatives and tasks in the corresponding design
dataset.
Define base case
We have to start by defining a base case, i.e. a
scenario that we want to start with.
#define a set of offerings
testm_pizza =
tibble(
id=1L, task=1L, alt=1:6,
brand = c("DiGi", "Fresc", "Priv", "RedBa", "Tomb", "Tony"),
size = "forOne",
crust = "Thin",
topping = "Veg",
coverage= "ModCover",
cheese = "NoInfo",
p = c(3.5,3,2,2,2,1.5)) %>%
prep_newprediction(pizza)
#for this experiment, offer this assortment to each of the respondents
testmarket=
tibble(
id = rep(seq_len(n_distinct(pizza$id)),each=nrow(testm_pizza)),
task = 1,
alt = rep(1:nrow(testm_pizza),n_distinct(pizza$id))) %>%
bind_cols(
testm_pizza[rep(1:nrow(testm_pizza),n_distinct(pizza$id)),-(1:3)])Demand curves
The output of ec_demcurve is a list, containing demand
summaries for each product under the different price scenarios. The list
can be stacked into a data.frame, which can be used to generate
plots.
#Define focal brand for analysis
focal_alternatives <-
testmarket %>% transmute(focal=brand=='Priv') %>% pull(focal)
#pre-sim error terms
eps_not <- testmarket %>% ec_gen_err_ev1(out_pizza_cal, 55667)
#demand curve compensatory
vd_demc_comp <-
testmarket %>%
ec_demcurve(focal_alternatives,
seq(0.5,1.5,,9),
vd_dem_vdm,
out_pizza_cal,
eps_not)
#demand curve conjunctive screening
vd_demc_screen <-
testmarket %>%
ec_demcurve(focal_alternatives,
seq(0.5,1.5,,9),
vd_dem_vdm_screen,
out_pizza_screening_cal,
eps_not)
#combine demand curves from both models
vd_outputs=rbind(
vd_demc_comp %>% do.call('rbind',.) %>% bind_cols(model='comp') %>% bind_cols(demand='volumetric'),
vd_demc_screen %>% do.call('rbind',.) %>% bind_cols(model='screenpr') %>% bind_cols(demand='volumetric'))
#plot
vd_outputs%>%
filter(brand=="Priv") %>%
ggplot(aes(x=scenario, y=`E(demand)`, color=model)) + geom_line(size=2, alpha=.7) +
xlab("Price (as % of original)") +
scale_x_continuous(labels = scales::percent_format(), n.breaks = 5) +
theme_minimal()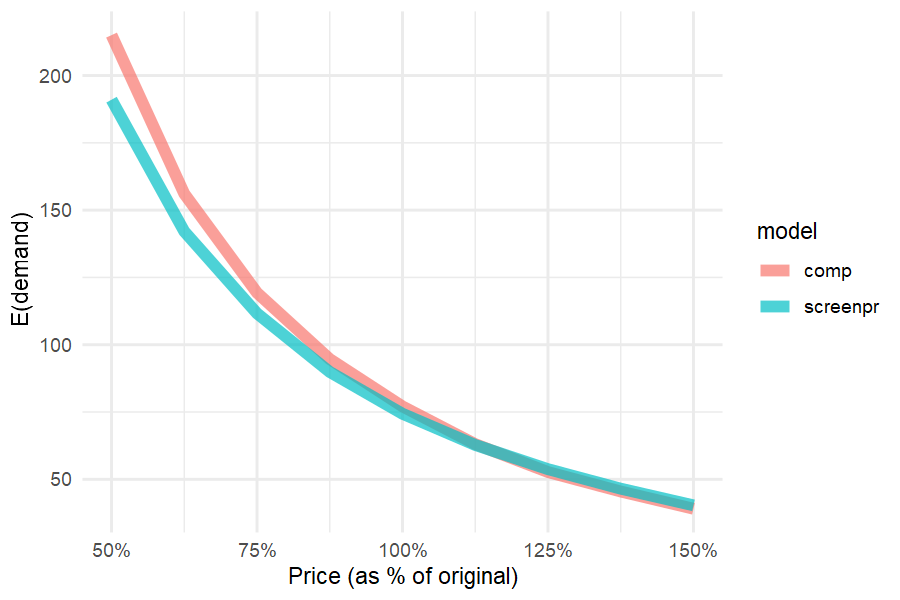
Incidence curves
While demand curves look similar, incidence curves reveal that drastic price decreases lead to a smaller increase in people buying when accounting for screening:
#demand curve compensatory
vd_demc_comp_inci =
testmarket %>%
ec_demcurve_inci(focal_alternatives,
seq(0.25,1.5,,9),
vd_dem_vdm,
out_pizza_cal,
eps_not)
#demand curve conjunctive screening
vd_demc_screen_inci =
testmarket %>%
ec_demcurve_inci(focal_alternatives,
seq(0.25,1.5,,9),
vd_dem_vdm_screen,
out_pizza_screening_cal,
eps_not)
#combine demand curves from both models
vd_outputs_inci=rbind(
vd_demc_comp_inci %>% do.call('rbind',.) %>% bind_cols(model='comp') %>% bind_cols(demand='volumetric'),
vd_demc_screen_inci %>% do.call('rbind',.) %>% bind_cols(model='screenpr') %>% bind_cols(demand='volumetric')) %>%
mutate(`E(purchase)`=`E(demand)`)
#plot
vd_outputs_inci%>%
filter(brand=="Priv") %>%
ggplot(aes(x=scenario, y=`E(purchase)`, color=model)) + geom_line(size=2, alpha=.7) +
xlab("Price (as % of original)") +
scale_x_continuous(labels = scales::percent_format(), n.breaks = 5) +
theme_minimal()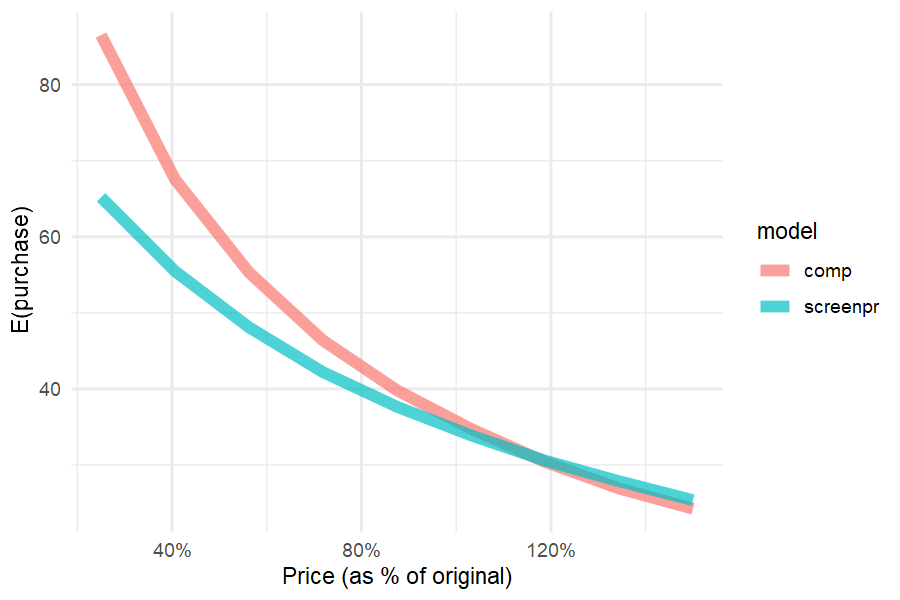
Incidence curves for all brands
Generating the same plot for all major brands, we can see differences in incidence between the different models.
allbrands=names(table(testmarket$brand))
demcout=list()
for(kk in 1:6){
demcout[[kk]]=
ec_demcurve_inci(testmarket,
testmarket$brand==allbrands[kk],
c(.5,.6,.7,.8,.9,1),
vd_dem_vdm_screen,
out_pizza_screening_cal,
ec_gen_err_ev1(testmarket,out_pizza_screening_cal,seed = 34543563))
}
demcout_vd=list()
for(kk in 1:6){
demcout_vd[[kk]]=
ec_demcurve_inci(testmarket,
testmarket$brand==allbrands[kk],
c(.5,.6,.7,.8,.9,1),
vd_dem_vdm,
out_pizza_cal,
ec_gen_err_ev1(testmarket,out_pizza_cal,seed = 34543563))
}
names(demcout)=allbrands
names(demcout_vd)=allbrands
demcurves_pizza=
demcout %>% purrr::map_dfr(. %>% do.call('rbind',.),.id='focal') %>%
filter(focal==brand) %>% bind_cols(model='with screening') %>%
bind_rows(
demcout_vd %>% purrr::map_dfr(. %>% do.call('rbind',.),.id='focal') %>%
filter(focal==brand) %>% bind_cols(model='without screening'))
demcurves_pizza %>%
mutate(model=factor(model,levels=c('without screening',"with screening"))) %>%
ggplot(aes(x=scenario,y=`E(demand)`, linetype=model)) +
geom_line() +
facet_wrap(~focal, scales = 'free_y') +
xlab("Price (as % of original)") + ylab('Number of people buying') +
scale_x_continuous(labels = scales::percent_format(), n.breaks = 3) + theme_minimal()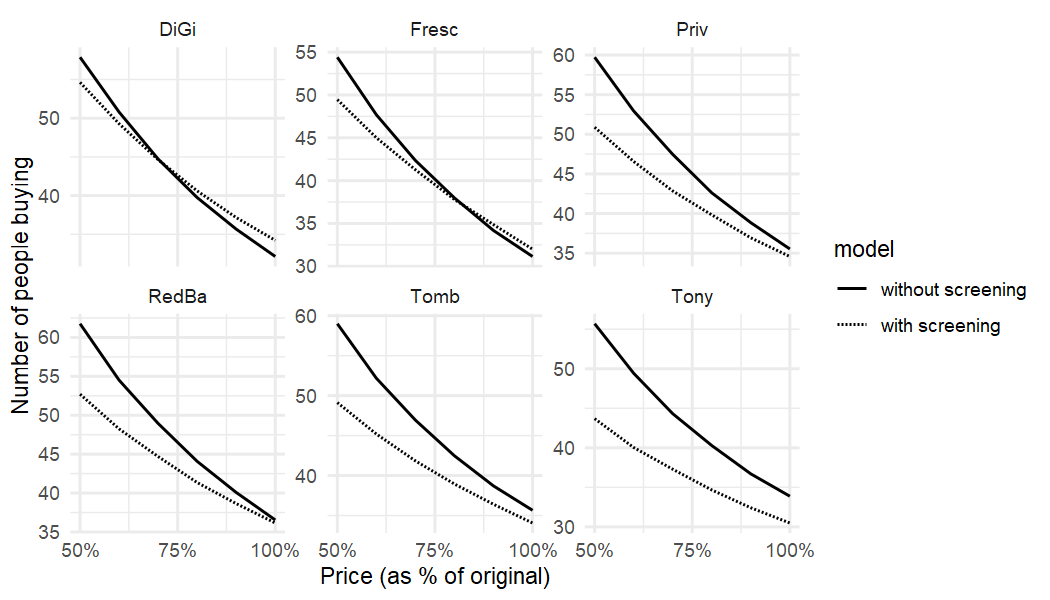
The role of screening
Frozen Pizza Consideration Set Size
To understand the pervasiveness of screening, we show the effective size of a consideration set, i.e. how many alternatives out of the 6 presented ones are actively evaluated by respondents. Unsurprisingly, it is a lot smaller than 6 for most.
vd_screenpr_n_screen=
pizza_cal%>%
ec_screenprob_sr(out_pizza_screening_cal) %>%
group_by(id, task) %>%
summarise(.screendraws=list(purrr::reduce(.screendraws ,`+`)), .groups = "keep") %>%
ec_screen_summarise %>%
group_by(id) %>%
summarise(n_screen=mean(`E(screening)`))
vd_screenpr_n_screen %>%
mutate(`Average size of consideration set`= 6-n_screen) %>%
ggplot(aes(x=`Average size of consideration set`)) +
geom_density(fill="lightgrey", linewidth=1) +
geom_vline(xintercept=6, linewidth=1.5, color="black") + theme_minimal()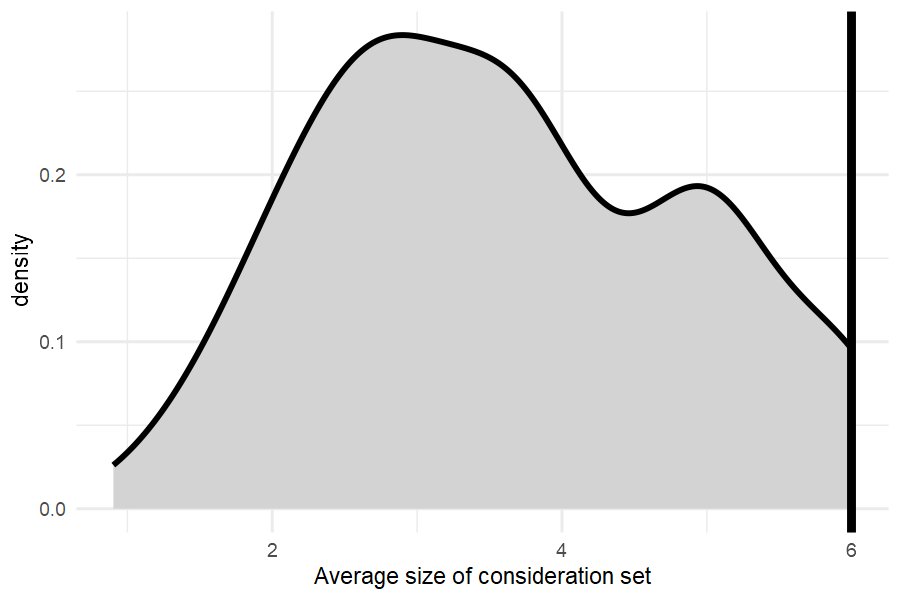
Predicting zero demand - Screening vs Preference
To further illustrate the relevance ofs creening, we can see how most of Tony’s non-buyeers simply do not even consider the brand.
#predict demand for base case
sim1_dem_vdscreen=
testm_pizza %>%
vd_dem_vdm_screen(out_pizza_screening_cal)
#(no-)buy probability
sim1_nobuy_vdsrpr=
sim1_dem_vdscreen %>%
mutate(draws=purrr::map(.demdraws,sign)) %>%
mutate(buyprob=purrr::map_dbl(.demdraws,mean)) %>%
group_by(brand) %>%
summarise(nobuy=1-mean(buyprob))
#screening probability
sim1_screen_vdsrpr=
testmarket %>%
ec_screenprob_sr(out_pizza_screening_cal) %>%
ec_screen_summarise %>% dplyr::select(-.screendraws) %>%
group_by(brand) %>%
summarise(screening=mean(`E(screening)`))
#create stacked plot
sim1_screen_vdsrpr %>%
left_join(sim1_nobuy_vdsrpr) %>%
mutate(`no preference`=nobuy-screening) %>%
dplyr::select(brand,screening,`no preference`) %>%
tidyr::pivot_longer(2:3,values_to = 'share', names_to = 'Explanation') %>%
mutate(`Alternative`=brand, `Share of 0-demand`=share) %>%
ggplot(aes(x=Alternative,y=`Share of 0-demand`,fill=Explanation)) +
geom_bar(stat='identity') +
scale_fill_grey(start=.7, end=.4, breaks=c('screening','no preference')) +
geom_text(aes(label = sprintf("%1.0f%%", 100*share)),
size = 4, hjust = 0.5, vjust = 0,
position = position_stack(vjust = 0.5)) +
scale_y_continuous(labels = scales::percent_format()) + theme_minimal() 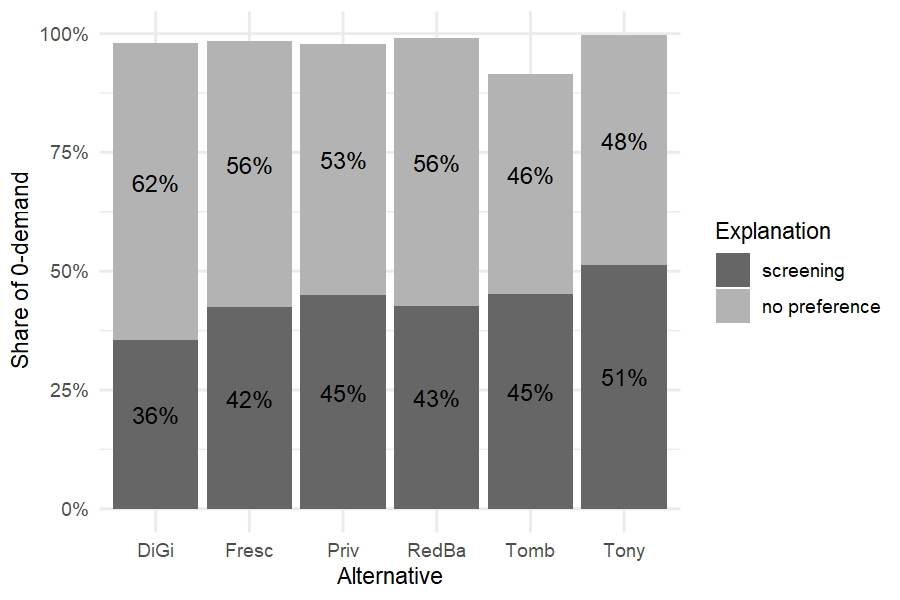
Relationship between screening and preference
We find that respondents with high screening probabilities tend to have \(\beta_{veg}\) close to the mode, indicating that individual-level information about preferences is not available when screening is present. More extreme estimates of \(\beta_{veg}\) occur when screening is not present. Thus, non-purchase is not rationalized as screening when there exists sufficient individual-level information to estimate preference.
scatterpl<-
tibble(id=seq_along(unique(pizza$id)),
beta = out_pizza_screening_cal$thetaDraw[15,,] %>% apply(1,mean),
tau = out_pizza_screening_cal$tauDraw[18,,] %>% apply(1,mean)) %>%
ggplot(aes(x=beta, y=tau)) +
geom_point(alpha=.3) + theme_minimal()
scatterplplus<-ggExtra::ggMarginal(scatterpl, type = "histogram")
print(scatterplplus)