Importing list-of-lists choice data and discrete choice modeling with echoice2
Source:vignettes/Importing_lol_data.Rmd
Importing_lol_data.RmdBackground
Many users have organized their choice data in a list-of-lists
format, where a list of length “number of respondents” is
created, and each element of that lists contains another list with
design matrix and choice information. An example of this is the
camera dataset in ‘bayesm’. echoice2 contains some helper
functions that make it easy to import such data, and estimate
corresponding discrete choice models.
Installation
The echoice2 package is available from CRAN and GitHub.
To install from CRAN, run:
install.packages("echoice2")To install the latest development version from GitHub run:
remotes::install_github("ninohardt/echoice2")Getting started
Load the package.
Key functions for using the package are:
-
vd_est_vdm: Estimating the “standard” volumetric demand model -
vd_est_vdm_screen: Estimating volumetric demand model with screening -
vd_dem_vdm: Demend predictions for the “standard” volumetric demand model -
vd_dem_vdm_screen: Demend predictions for the volumetric demand model with screening
Functions that relate to discrete demand start in dd_,
while functions for volumetric demand start in vd_.
Estimation functions continue in est, demand simulators in
dem. Universal functions (discrete and volumetric choice)
start in ec_.
Data organization
Choice data should be provided in a ‘long’ format tibble or data.frame, i.e. one row per alternative, choice task and respondent.
It should contain the following columns
-
id(integer; respondent identifier) -
task(integer; task number) -
alt(integer; alternative #no within task) -
x(double; quantity purchased) -
p(double; price) - attributes defining the choice alternatives (factor, ordered) and/or
- continuous attributes defining the choice alternatives (numeric)
By default, it is assumed that respondents were able to choose the ‘outside good’, i.e. there is a ‘no-choice’ option. The no-choice option should not be explicitly stated, i.e. there is no “no-choice-level” in any of the attributes. This differs common practice in discrete choice modeling, however, the implicit outside good is consistent with both volumetric and discrete choice models based on economic assumptions.
Dummy-coding is performed automatically to ensure consistency between
estimation and prediction, and to set up screening models in a
consistent manner. Categorical attributes should therefore be provided
as factor or ordered, and not be
dummy-coded.
Importing list-of-list data
Let’s consider the camera example dataset from bayesm.
library(bayesm)
data(camera)
head(camera[[1]]$X)
#> canon sony nikon panasonic pixels zoom video swivel wifi price
#> 1 0 0 1 0 0 1 0 1 0 0.79
#> 2 1 0 0 0 1 1 0 1 1 2.29
#> 3 0 0 0 1 0 0 0 0 1 1.29
#> 4 0 1 0 0 0 1 0 1 0 2.79
#> 5 0 0 0 0 0 0 0 0 0 0.00
#> 6 0 0 0 1 1 0 0 1 0 2.79
head(camera[[1]]$y)
#> [1] 1 2 2 4 2 2Now let’s prepare this dataset for analysis with ‘echoice2’. Using
ec_lol_tidy1 we can stack information from all respondents.
The price variable is renamed to p.
data_tidier <- ec_lol_tidy1(camera) %>% rename(`p`='price')
data_tidier %>% head
#> # A tibble: 6 × 14
#> id task alt canon sony nikon panasonic pixels zoom video swivel wifi p x
#> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 1 1 0 0 1 0 0 1 0 1 0 0.79 1
#> 2 1 1 2 1 0 0 0 1 1 0 1 1 2.29 0
#> 3 1 1 3 0 0 0 1 0 0 0 0 1 1.29 0
#> 4 1 1 4 0 1 0 0 0 1 0 1 0 2.79 0
#> 5 1 1 5 0 0 0 0 0 0 0 0 0 0 0
#> 6 1 2 1 0 0 0 1 1 0 0 1 0 2.79 0Looking into the p column, we can see that the 5th
alternative in each task has a price of 0. This is an
explicit outside good which needs to be removed:
data_tidier_2 <- data_tidier %>% filter(p>0)
data_tidier_2 %>% head
#> # A tibble: 6 × 14
#> id task alt canon sony nikon panasonic pixels zoom video swivel wifi p x
#> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 1 1 0 0 1 0 0 1 0 1 0 0.79 1
#> 2 1 1 2 1 0 0 0 1 1 0 1 1 2.29 0
#> 3 1 1 3 0 0 0 1 0 0 0 0 1 1.29 0
#> 4 1 1 4 0 1 0 0 0 1 0 1 0 2.79 0
#> 5 1 2 1 0 0 0 1 1 0 0 1 0 2.79 0
#> 6 1 2 2 1 0 0 0 1 0 1 0 1 0.79 1We can already see a couple of brand dummies, which need to be “un-dummied” into a categorical variable. Let’s first check if there are more attributes in dummy form by checking mutually exlusive attributes:
data_tidier_2 %>% ec_util_dummy_mutualeclusive() %>% filter(mut_ex)
#> # A tibble: 6 × 3
#> V1 V2 mut_ex
#> <chr> <chr> <lgl>
#> 1 canon sony TRUE
#> 2 canon nikon TRUE
#> 3 canon panasonic TRUE
#> 4 sony nikon TRUE
#> 5 sony panasonic TRUE
#> 6 nikon panasonic TRUEAs we can see, only brand names come up. “Un-dummying” it is easy
using the ec_undummy function. It has to be supplied with
the column names of the dummies to be un-dummied, and the name of the
target variable, in this case “brand”.
data_tidier_3 <-
data_tidier_2 %>% ec_undummy(c('canon','sony','nikon','panasonic'), 'brand')
data_tidier_3 %>% head
#> # A tibble: 6 × 11
#> id task alt brand pixels zoom video swivel wifi p x
#> <chr> <int> <int> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 1 1 nikon 0 1 0 1 0 0.79 1
#> 2 1 1 2 canon 1 1 0 1 1 2.29 0
#> 3 1 1 3 panasonic 0 0 0 0 1 1.29 0
#> 4 1 1 4 sony 0 1 0 1 0 2.79 0
#> 5 1 2 1 panasonic 1 0 0 1 0 2.79 0
#> 6 1 2 2 canon 1 0 1 0 1 0.79 1The remaining dummies are either high-low or yes-no type binary
attributes. The two utility functions ec_undummy_lowhigh
and ec_undummy_yesno make it convenient to undummy these as
well:
data_tidied<-
data_tidier_3 %>%
mutate(across(c(pixels,zoom), ec_undummy_lowhigh))%>%
mutate(across(c(swivel,video,wifi), ec_undummy_yesno))
data_tidied %>% head()
#> # A tibble: 6 × 11
#> id task alt brand pixels zoom video swivel wifi p x
#> <chr> <int> <int> <fct> <fct> <fct> <fct> <fct> <fct> <dbl> <dbl>
#> 1 1 1 1 nikon low high no yes no 0.79 1
#> 2 1 1 2 canon high high no yes yes 2.29 0
#> 3 1 1 3 panasonic low low no no yes 1.29 0
#> 4 1 1 4 sony low high no yes no 2.79 0
#> 5 1 2 1 panasonic high low no yes no 2.79 0
#> 6 1 2 2 canon high low yes no yes 0.79 1Now data_tidied is ready for analysis.
Checking data
To verify attributes and levels, we can use
ec_summarize_attrlvls:
data_tidied %>% ec_summarize_attrlvls
#> # A tibble: 6 × 2
#> attribute levels
#> <chr> <chr>
#> 1 brand canon, nikon, panasonic, sony
#> 2 pixels low, high
#> 3 zoom low, high
#> 4 video no, yes
#> 5 swivel no, yes
#> 6 wifi no, yesSince we have an implicit outside good, let’s check that task total exhibit variation:
data_tidied %>%
group_by(id, task) %>%
summarise(x_total = sum(x), .groups = "keep") %>%
group_by(x_total) %>% count(x_total)
#> # A tibble: 2 × 2
#> # Groups: x_total [2]
#> x_total n
#> <dbl> <int>
#> 1 0 1343
#> 2 1 3969Holdout
For hold-out validation, we keep 1 task per respondent. In v-fold cross-validation, this is done several times. However, each re-run of the model may take a while. For this example, we only use 1 set of holdout tasks. Hold-out evaluations results may vary slightly between publications that discuss this dataset.
#randomly assign hold-out group, use seed for reproducible plot
set.seed(555)
data_ho_tasks=
data_tidied %>%
distinct(id,task) %>%
mutate(id=as.integer(id))%>%
group_by(id) %>%
summarise(task=sample(task,1), .groups = "keep")
set.seed(NULL)
#calibration data
data_cal= data_tidied %>% mutate(id=as.integer(id)) %>%
anti_join(data_ho_tasks, by=c('id','task'))
#'hold-out' data
data_ho= data_tidied %>% mutate(id=as.integer(id)) %>%
semi_join(data_ho_tasks, by=c('id','task'))Estimation
Estimate both models using at least 200,000 draws. Saving
each 50th or 100th draw is sufficient. The vd_est_vdm fits
the compensatory volumetric demand model, while
vd_est_vdm_screen fits the model with attribute-based
conjunctive screening. Using the error_dist argument, the
type of error distribution can be specified. While KHKA 2022
assume Normal-distributed errors, here we assume Extreme Value Type 1
errors.
#compensatory
out_camera_compensatory <- dd_est_hmnl(data_tidied)
dir.create("draws")
save(out_camera_compensatory,file='draws/out_camera_cal.rdata')
#conjunctive screening
out_camera_screening <- dd_est_hmnl_screen(data_tidied)
save(out_camera_screening,file='draws/out_camera_screening.rdata')Diagnostics
Quick check of convergence, or stationarity of the traceplots.
Compensatory:
out_camera_compensatory %>% ec_trace_MU(burnin = 100)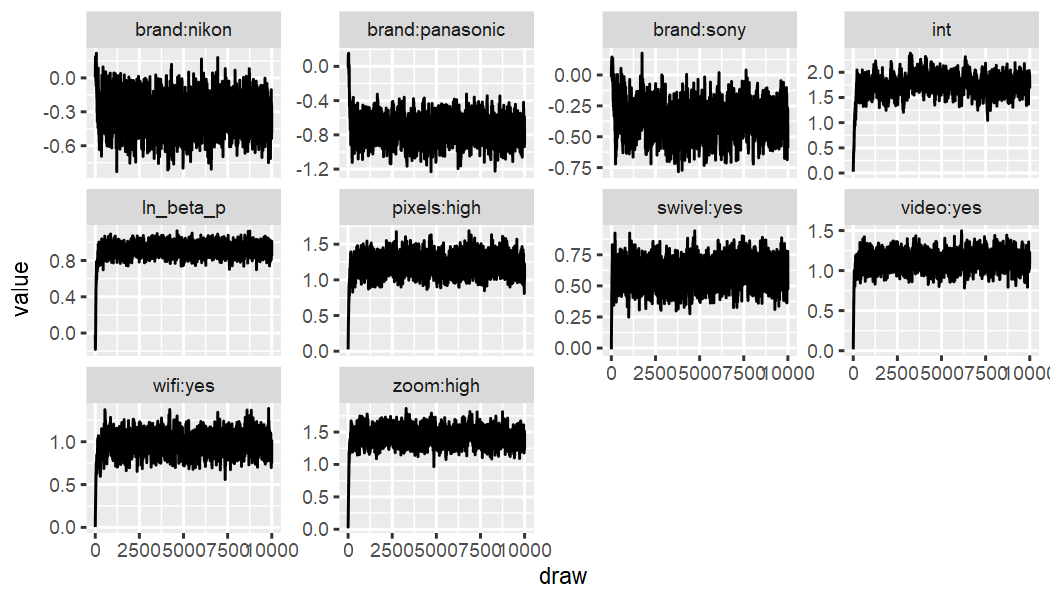
Conjunctive Screening:
out_camera_screening %>% ec_trace_MU(burnin = 100)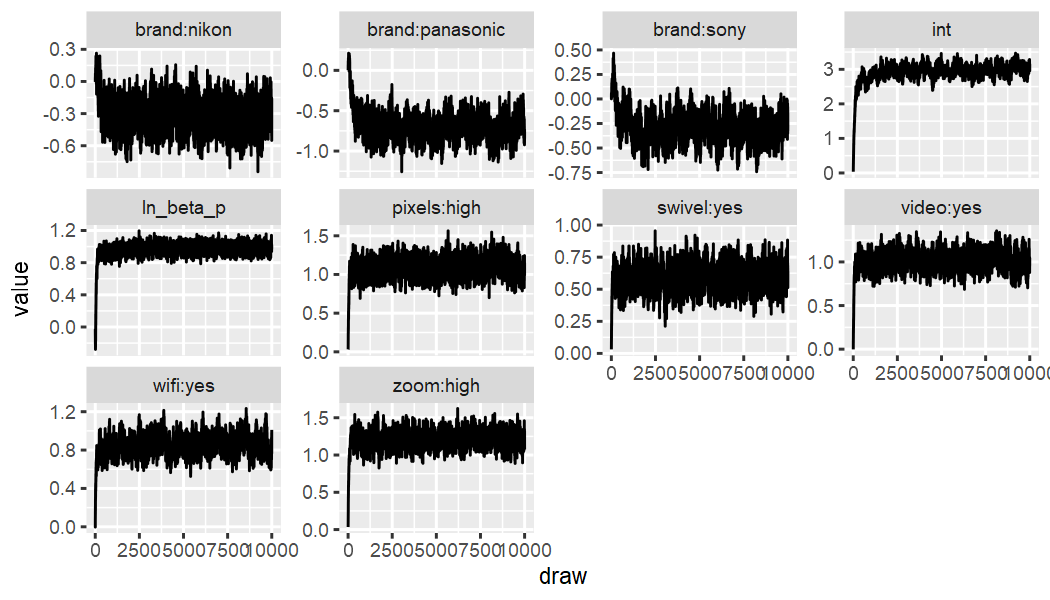
Distribution of Log-likehoods to check for outlier respondents:
dd_LL(out_camera_compensatory ,data_cal, fromdraw = 3000) %>%
apply(1,mean) %>% tibble(LL=.) %>%
ggplot(aes(x=LL)) +
geom_density(fill="lightgrey", linewidth=1) + theme_minimal() +
xlab("Individual average Log-Likelihood")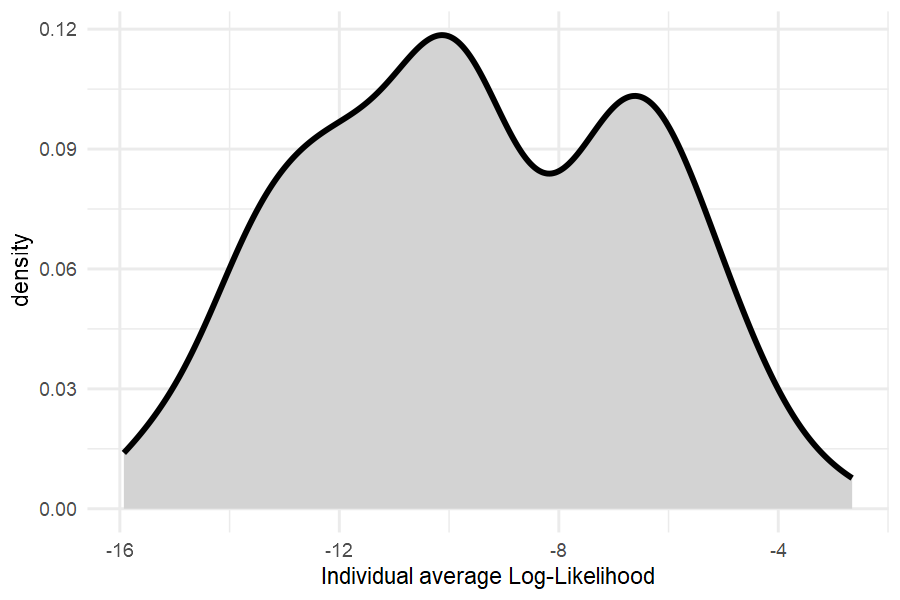
All average log-likelihoods are better than random selection, indicating good data quality.
Fit
Holdout
Now, we compare “holdout”-fit. Here we obtain posterior distributions
of choice share predictions via dd_dem and
dd_dem_sr and then compute the hit probabilities. It is
adviced to carefully think about your relevant loss function and choose
an appropriate metric for holdout fit comparisons.
ho_prob_dd=
data_ho %>%
prep_newprediction(data_cal) %>%
dd_dem(out_camera_compensatory, prob=TRUE)
ho_prob_ddscreen=
data_ho %>%
prep_newprediction(data_cal) %>%
dd_dem_sr(out_camera_screening, prob=TRUE)
hit_probabilities=c()
hit_probabilities$compensatory=
ho_prob_dd %>%
vd_dem_summarise() %>%
select(id,task,alt,x,p,`E(demand)`) %>%
group_by(id,task) %>% group_split() %>%
purrr::map_dbl(. %>% select(c(x,`E(demand)`)) %>%
add_row(x=1-sum(.$x),`E(demand)`=1-sum(.$`E(demand)`)) %>%
summarise(hp=sum(x*`E(demand)`))%>% unlist) %>% mean()
hit_probabilities$screening=
ho_prob_ddscreen %>%
vd_dem_summarise() %>%
select(id,task,alt,x,p,`E(demand)`) %>%
group_by(id,task) %>% group_split() %>%
purrr::map_dbl(. %>% select(c(x,`E(demand)`)) %>%
add_row(x=1-sum(.$x),`E(demand)`=1-sum(.$`E(demand)`)) %>%
summarise(hp=sum(x*`E(demand)`))%>% unlist) %>% mean()
hit_probabilities
#> $compensatory
#> [1] 0.4294928
#>
#> $screening
#> [1] 0.4666976Estimates
Part-Worths
Using ec_estimates_MU it is easy to obtain the “upper
level” posterior means of the key parameters. We can see that Canon is
the most popular brand. All brand “part-worths” are larger when
accounting for screening, but it is particularly noticeable for Sony and
Panasonic.
out_camera_compensatory %>% ec_estimates_MU()
#> # A tibble: 10 × 12
#> attribute lvl par mean sd `CI-5%` `CI-95%` sig model error reference_lvl parameter
#> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <lgl> <chr> <chr> <chr> <chr>
#> 1 brand nikon brand:nikon -0.322 0.134 -0.538 -0.103 TRUE hmnl-comp EV1 canon nikon
#> 2 brand panasonic brand:panasonic -0.736 0.139 -0.945 -0.527 TRUE hmnl-comp EV1 canon panasonic
#> 3 brand sony brand:sony -0.360 0.126 -0.557 -0.151 TRUE hmnl-comp EV1 canon sony
#> 4 pixels high pixels:high 1.22 0.128 1.03 1.41 TRUE hmnl-comp EV1 low high
#> 5 zoom high zoom:high 1.43 0.126 1.25 1.61 TRUE hmnl-comp EV1 low high
#> 6 video yes video:yes 1.12 0.106 0.958 1.28 TRUE hmnl-comp EV1 no yes
#> 7 swivel yes swivel:yes 0.597 0.0931 0.448 0.750 TRUE hmnl-comp EV1 no yes
#> 8 wifi yes wifi:yes 0.980 0.114 0.801 1.16 TRUE hmnl-comp EV1 no yes
#> 9 <NA> <NA> int 1.74 0.199 1.47 2.02 TRUE hmnl-comp EV1 <NA> int
#> 10 <NA> <NA> ln_beta_p 0.919 0.0809 0.821 1.01 TRUE hmnl-comp EV1 <NA> ln_beta_p
out_camera_screening %>% ec_estimates_MU()
#> # A tibble: 10 × 12
#> attribute lvl par mean sd `CI-5%` `CI-95%` sig model error reference_lvl parameter
#> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <lgl> <chr> <chr> <chr> <chr>
#> 1 brand nikon brand:nikon -0.309 0.143 -0.536 -0.0680 TRUE hmnl-conj-pr EV1 canon nikon
#> 2 brand panasonic brand:panasonic -0.687 0.163 -0.920 -0.448 TRUE hmnl-conj-pr EV1 canon panasonic
#> 3 brand sony brand:sony -0.284 0.149 -0.509 -0.0405 TRUE hmnl-conj-pr EV1 canon sony
#> 4 pixels high pixels:high 1.08 0.120 0.904 1.27 TRUE hmnl-conj-pr EV1 low high
#> 5 zoom high zoom:high 1.21 0.115 1.04 1.38 TRUE hmnl-conj-pr EV1 low high
#> 6 video yes video:yes 1.01 0.107 0.852 1.18 TRUE hmnl-conj-pr EV1 no yes
#> 7 swivel yes swivel:yes 0.588 0.0935 0.438 0.740 TRUE hmnl-conj-pr EV1 no yes
#> 8 wifi yes wifi:yes 0.852 0.104 0.692 1.02 TRUE hmnl-conj-pr EV1 no yes
#> 9 <NA> <NA> int 2.92 0.263 2.59 3.21 TRUE hmnl-conj-pr EV1 <NA> int
#> 10 <NA> <NA> ln_beta_p 0.965 0.0899 0.873 1.06 TRUE hmnl-conj-pr EV1 <NA> ln_beta_pScreening probabilities
Using ec_estimates_screen, screening probabilities be
obtained. As we can see, screening does not play a huge role in this
dataset, and therefore improvements in fit are just modest.
out_camera_screening %>% ec_estimates_screen()
#> # A tibble: 14 × 8
#> attribute lvl par mean sd `CI-5%` `CI-95%` limit
#> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 brand canon brand:canon 0.0247 0.0489 0.00572 0.0402 NA
#> 2 brand nikon brand:nikon 0.0169 0.0495 0.00122 0.0308 NA
#> 3 brand panasonic brand:panasonic 0.0419 0.0497 0.0107 0.0735 NA
#> 4 brand sony brand:sony 0.0395 0.0490 0.0108 0.0656 NA
#> 5 pixels high pixels:high 0.00922 0.0495 0.000257 0.0133 NA
#> 6 pixels low pixels:low 0.0635 0.0466 0.0343 0.0882 NA
#> 7 swivel no swivel:no 0.0315 0.0483 0.0115 0.0469 NA
#> 8 swivel yes swivel:yes 0.0143 0.0492 0.00193 0.0218 NA
#> 9 video no video:no 0.0474 0.0472 0.0239 0.0672 NA
#> 10 video yes video:yes 0.00837 0.0495 0.000182 0.0106 NA
#> 11 wifi no wifi:no 0.0692 0.0462 0.0400 0.0941 NA
#> 12 wifi yes wifi:yes 0.0181 0.0490 0.00372 0.0276 NA
#> 13 zoom high zoom:high 0.0130 0.0493 0.00125 0.0191 NA
#> 14 zoom low zoom:low 0.0929 0.0454 0.0584 0.123 NA